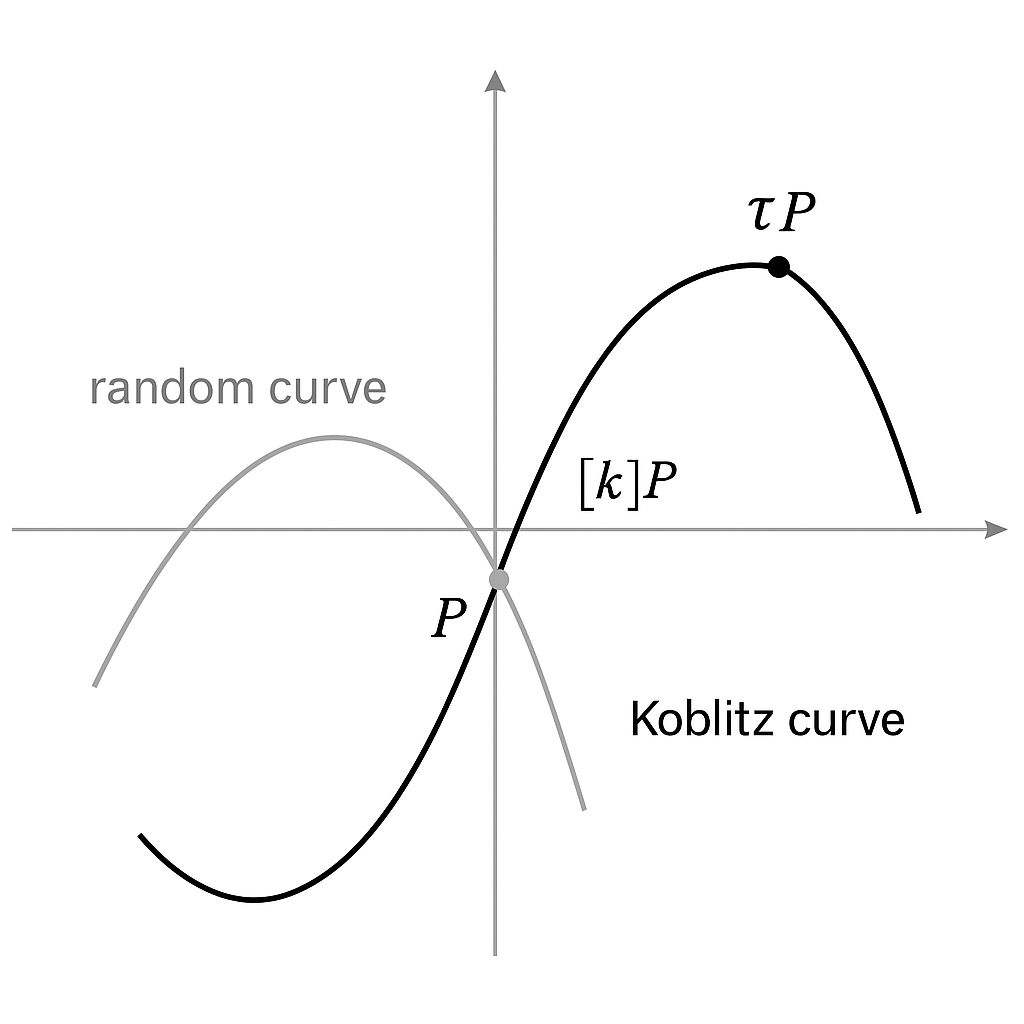
Why koblitz is faster than random
안녕하세요. 오늘은 암호학에서 자주 등장하는 두 종류의 타원곡선—Koblitz 곡선과 일반적인 랜덤 타원곡선(일명 random curve)—이 왜 scalar multiplication(스칼라배) 연산에서 차이를 보이는가에 대해 이야기해볼까 합니다.
서론
타원곡선 암호(ECC: Elliptic Curve Cryptography)에서는 “한 점을 여러 번 더한다(= 스칼라배)”는 연산이 굉장히 핵심적인 변환이 됩니다.
예컨대 어떤 곡선 위의 점 $P$에 대해 정수 $k$를 곱한다는 것은
이라는 의미로 볼 수 있고요.
이 연산이 곧 암호 체계의 ‘지불(연산) 비용’을 결정짓는 중요한 요소가 됩니다.
그런데 같은 보안 수준(예컨대 약 $2^{256}$ 수준의 난이도)을 갖는 곡선이라 할지라도, Koblitz 곡선 쪽이 일반적인(랜덤하게 선택한) 곡선보다 스칼라배 연산이 상당히 빠른 경우가 있습니다.
왜 그런 차이가 발생하는지, 그 원리를 차근차근 풀어보겠습니다.
1. 일반 곡선에서 스칼라배이 느린 이유
우선 일반적인 타원곡선(보통 소수체 $\mathbb F_p$ 위에 정의된 곡선)을 생각해볼게요.
이런 곡선 위에서 스칼라배 연산을 수행하면 다음과 같은 흐름을 따릅니다.
- 먼저 스칼라 $k$를 이진 표현으로 바꿉니다.
예컨대 $k = (b_n b_{n-1} \dots b_1 b_0)_2$. - 그리고 반복적으로 다음을 수행합니다.
- 현재 점을 두 배(Double)한다.
- 만약 해당 비트 $b_i = 1$이면 덧셈(Add) 연산을 한다.
- 이 과정을 통해 결국 $[k]P$를 구하게 됩니다.
왜 이 방식이 느릴까요? 크게 두 가지 이유가 있습니다.
- 이중화 + 덧셈이 반복되기 때문에 연산량이 많습니다.
이중화도 간단한 연산은 아니고, 덧셈도 곡선 위에서 좌표 연산(역수 계산 등)을 동반합니다. - 병렬화가 어렵습니다. 연산이 순차적입니다. ‘현재 점’이 생긴 뒤에야 다음 단계로 넘어가야 하며, 이전 단계가 끝나야 다음이 가능하므로 병렬 처리 이점이 거의 없습니다.
결국, 일반 곡선에서 스칼라배는 계산 비용이 비교적 큰 연산이며, 구현체나 최적화를 잘 해야 성능이 나옵니다.
2. Koblitz 곡선이란 무엇인가?
이제 Koblitz 곡선을 이야기해볼 차례입니다.
이 곡선은 Neal Koblitz가 제안한 특수한 형태의 타원곡선으로, 특징은 다음과 같습니다.
- 정의체(field)가 이진체(binary field) $\mathbb F_{2^m}$ 위에 정의됩니다.
- 곡선 방정식이 보통의 형태 $y^2 = x^3 + ax + b$ 보다는 조금 다르게, 예컨대
와 같은 형태를 가질 수 있고요.
- 무엇보다 중요한 것은 이 곡선 위에는 Frobenius 자기사상(Frobenius endomorphism)이라는 매우 유리한 구조가 존재한다는 점입니다.
이 구조 덕분에, 스칼라배 연산을 일반 곡선 방식보다 훨씬 더 효율적으로 구현할 수 있게 됩니다.
3. Frobenius 자기사상이란 무엇인가?
‘자기사상’이라는 말이 다소 낯설 수 있지만, 개념은 생각보다 직관적입니다.
이진체 $\mathbb F_{2^m}$ 위의 요소(element)는 다항식 표현으로 볼 수 있고, 이 다항식의 각 항(비트)을 제곱하는 연산이 널리 쓰입니다.
정확히 말하면 아래와 같은 함수입니다.
이 연산이 중요한 이유는 다음과 같습니다.
- 이진체에서는 “제곱 연산”이 매우 빠릅니다. 다항식 표현에서 각각의 항을 제곱하는 것은 비트 시프트나 단순한 자리 변환 수준으로 볼 수 있어서, 비교적 비용이 작습니다.
- 이진체 위에서의 곱셈 연산의 경우 $O(m\log m)$의 시간복잡도를 갖는 반면 제곱 연산의 경우 모든 교차항이 사라지기 때문에 ($2\equiv 0$) 이진체의 각각의 항에 대해 제곱한 항만 남게 됩니다. 즉, 시간복잡도는 $O(m)$이 되게 됩니다.
- 이 자기사상 $\tau$는 곡선 위의 점을 또 다른 점으로 보내는 곡선 자체의 선형 변환(endomorphism)이기 때문에, 스칼라배 연산에 응용 가능하다는 점이 핵심입니다.
즉, 일반 곡선에서는 “점 × 2”라면, Koblitz 곡선에서는 “점에 $\tau$ 적용”이라는 더 가볍고 특별한 2배 역할을 하는 연산으로 대체할 수 있는 셈이 됩니다.
4. τ-스칼라배 방식과 그로 인한 속도 향상
그렇다면 실제로 Koblitz 곡선 위에서 스칼라배 연산은 어떻게 바뀌는가 보겠습니다.
일반 곡선에서는 다음과 같이 표현됩니다.
여기서 각 $2^i$ 곱하기는 점을 반복해서 두 배하는 과정을 의미합니다.
반면 Koblitz 곡선에서는 이 구조를 아래와 같이 변환할 수 있습니다:
- 여기서 각 $c_i$는 일반적으로 $-1,\,0,\,1$ 중 하나인 계수(coefficient)입니다 (이를 τ-NAF(Tau Non-Adjacent Form) 라고 부릅니다).
- $\tau^i$는 $\tau$ 연산을 $i$번 반복 적용한 것, 즉 점에 여러 번 제곱 적용한 변형점입니다.
이 방식이 왜 빠른가를 정리하면:
- “2배 연산”이 아니라 “제곱 연산(= $\tau$ 적용)”으로 바뀌면서 비용이 훨씬 줄어듭니다.
- τ-NAF 표현 덕분에 $c_i = 0$인 경우가 많고, 덧셈(Add) 연산이 실제로 필요한 경우가 확 줄어듭니다.
- 더 나아가, $\tau^i P$들의 계산이 서로 간섭이 적기 때문에 병렬화 가능성이 높아집니다 — 즉 여러 코어 혹은 여러 하드웨어 단위에서 동시에 계산이 가능합니다.
결과적으로 Koblitz 곡선에서 스칼라배은 일반 곡선 대비 몇십 퍼센트 이상 빠른 경우가 실제 구현에서 확인되곤 합니다.
5. 병렬화 가능성: 왜 중요할까요?
처음 말씀드렸듯이 일반 곡선 방식에서는 ‘이중화 → 덧셈’이 순차적으로 이루어지기 때문에 병렬화가 거의 안 됩니다.
하지만 Koblitz 곡선 방식에서는 조금 다른 방식이 가능합니다:
- $\tau^0 P, \tau^1 P, \tau^2 P, \dots$ 처럼 서로 독립적인 변형점들을 미리 계산해 둘 수 있고,
- 이러한 계산이 서로 의존성이 적기 때문에 여러 유닛(코어, 하드웨어 스레드 등)에서 동시에 수행할 수 있습니다.
- 마지막에 이 변형점들을 계수 $c_i$에 맞춰 가중합하는 방식으로 스칼라배을 완성합니다.
즉, Koblitz 곡선 방식은 “병렬 연산에 적합한 구조”라고 볼 수 있고, 요즘처럼 멀티코어·GPU·FPGA 등을 활용하는 하드웨어 환경에서는 매우 큰 이점을 갖습니다.
6. 모든 곡선에 이 방식을 쓰지 않는 이유
그럼 “그렇다면 모든 타원곡선을 Koblitz 형태로 하면 되지 않느냐?”라는 의문이 생기실 법합니다.
하지만 현실은 그렇지 않습니다. 이유는 다음과 같습니다:
- Koblitz 곡선은 구조가 매우 특수합니다. 즉, 곡선을 정의할 때 자유도가 낮고, 곡선이 가진 수학적 형태가 많이 노출됩니다.
- 이로 인해 공격자가 이 구조적 특성을 악용할 가능성이 일반 곡선 대비 다소 높아질 수 있습니다. 예컨대 특정 이진체 공격 기법이나 구조 기반의 약점이 존재할 수 있고요.
- 따라서 암호 표준화 과정에서는 일반적으로 안정성을 우선하고, 속도는 그 다음 고려사항이 되는 경우가 많습니다.
예컨대 표준화된 소수체 기반 곡선들(예: P-256, P-384 등)은 랜덤하게 선택된 곡선 계수를 사용해서 구조적 예측 가능성을 줄인 형태이고, 이진체 기반 Koblitz 곡선(예: sect163k1, sect233k1 등)은 별도로 존재하는 형태입니다.
7. 요약 정리
아래 표는 일반 곡선과 Koblitz 곡선의 주요 차이를 정리한 것입니다.
| 항목 | 일반(랜덤) 곡선 | Koblitz 곡선 |
|---|---|---|
| 정의 필드 | 보통 소수체 $\mathbb F_p$ | 이진체 $\mathbb F_{2^m}$ |
| 스칼라배 방식 | 이중화(Double) → 덧셈(Add) 반복 | $\tau$ 적용 → 덧셈(Add) 방식 |
| 제곱/두 배 연산 비용 | 비교적 높음 | 제곱 연산이 매우 저렴 |
| 병렬화 가능성 | 거의 없음 | 매우 높음 |
| 속도 | 느림 | 빠름 |
| 구조적 예측 가능성·안정성 | 상대적으로 높음 | 구조가 드러날 가능성 있음 |
결론
결국, Koblitz 곡선이 랜덤 곡선보다 스칼라배 연산에서 더 빠른 이유는 특수한 수학적 구조 덕분입니다.
이진체 위에서 정의되어 제곱 연산이 저렴하고, Frobenius 자기사상 $\tau$라는 특별한 도구를 통해 일반 곡선의 이중화 연산을 대체할 수 있으며, 덧셈 횟수도 줄일 수 있고, 나아가 병렬화까지 활용 가능하게 되었습니다.
하지만 속도가 전부는 아닙니다. 암호학에서는 안전성이 무엇보다도 중요하고, 구조가 단순하면 단순할수록 예상치 못한 취약점이 나올 가능성도 생깁니다.
그래서 표준 곡선 설계에서는 이러한 트레이드오프(trade-off)를 신중하게 고려하게 됩니다.
오늘 글이 Koblitz 곡선과 일반 곡선의 차이, 그리고 그 속도 차이가 어디서 기인하는지를 이해하는 데 도움이 되었기를 바랍니다.
읽어주셔서 감사합니다!